Can anyone calculate by hand (without a calculator) the square root of 5.71 ? How about the two-dimensional complex number (4 + 2.53 i ) ?
Of course not. Normal people who are not mathematicians punch these numbers into calculators or math apps on their iPads and computers to calculate the answers.
Without iterating — that is: guessing, deriving a result, and then zeroing in with better guesses) — finding the square root of 5.71 requires knowledge of some arcane mathematics. No one labors by hand to find the answer, which is 2.38956… . It’s the principal square root, of course.
How does anyone iterate to derive the square root of the complex number (4 + 2.53 i ), which happens to be (2.0896… + .606375…i ) ? It is also a principal square root. What are the others? Is there more than two? People use calculators and pewters to find out; there is no easier way.
In high school and basic college math courses, people typically learn to solve algebraic equations. A typical algebraic equation looks like
![]() …right?
…right?
They have polynomials with integer coefficients. The solution is ![]() , which in this case is an algebraic irrational number. Equations like trig and log functions that transcend algebra (called transcendental equations) are taught maybe to engineers and science majors; math majors, of course, don’t struggle with this stuff. It’s why they are math majors.
, which in this case is an algebraic irrational number. Equations like trig and log functions that transcend algebra (called transcendental equations) are taught maybe to engineers and science majors; math majors, of course, don’t struggle with this stuff. It’s why they are math majors.
Several categories of transcendental equations are commonly encountered in the sciences. Many simple problems can be solved by Newton’s Method, which is taught in basic calculus. I won’t explain the method in this essay. Folks can click on links to learn more if they want.
A category of transcendental equations that can get complicated is of the general form
![]()
The biggest problems arise when “y” is known, but “x” isn’t. How to solve for “x”?
Any transcendental equation that is able to be transformed into the form xex can be solved for “x” using the Lambert W function. The equation can be inverted into the form, x = W(y). People are going to have to take my word, for now.
The math behind the Lambert function is mind-bogglingly complicated to most people. The function can sometimes require unusual and involved “series expansions” and transcendental-styled integrals that are not possible to solve easily or quickly without a computer.
The Lambert W function (sometimes referred to as the omega (ω) function or the product-logarithm function) is not a key or button that can be pushed on most calculators. However, math apps like Wolfram Alpha and Mathematica sometimes solve transcendental problems using the Lambert ω function in the background when the equations that need solving aren’t so easy.
I ran across a transcendental equation on the web that is perfectly suited to teach the “ω” method. Here it is:
![]()
I want to solve it to demonstrate how to use the ω method for transcendental functions that aren’t otherwise so easy to work out. I challenge anyone to solve this equation using Newton’s Method or other iterative techniques. Most will struggle to the point of pulling out their hair, probably. And they will waste time. Yes, it can be solved by those techniques.
We will solve this equation step by step using the Lambert method shortly. Meanwhile, here is the strategy:
1. Substitute an exponent function (et) for “x” everywhere in the expression.
2. Manipulate the equation into the form:
![]()
![]()
3. Invert the equation to introduce the ω function.
4. Use the ω function to solve for “t”.
5. Write out x = et using the expression derived for “t”.
6. Solve ω(y) using WolframAlpha or any other app with the capability.
7. Use the value of ω(y) to solve for “x”.
Each step of the strategy will be identified by numbers 1-7 in the solution below.
Here’s the thing:
In this problem it turns out that there are four ω values of y, which will generate two real solutions and two complex solutions. These omega values are:
ω0(y)
ω-1(y)
ω–2(y)
ω1(y)
WolframAlpha will generate all the solutions automatically; no need for the user to understand anything. People can punch in the original equation and trust the answers the app returns.
But the solution steps that follow are fashioned to demonstrate how the problem is solved when all anyone has is an algorithm to generate the values of the omega functions. Omega functions are difficult to solve without using certain algorithms involving integrals and expansion series on robust computers.
The process that surrounds the computation of omega values, which permit the working out of the appropriate values (the right answers) to the kind of equation I will soon solve is interesting and enlightening, at least for me, and hopefully for certain readers.
Some folks will appreciate the insights this exercise provides.
Having knowledge will make the Lambert process that is used to solve certain transcendental functions less mysterious. Of course, one can always take the time to learn the expansion series and integrals. In some cases, Newton’s Method can generate the values.
Unless humankind loses the technology of computers, I don’t think it is a good use of time and resources to learn the series, integrals, and algorithms that generate omega values.
Let’s face an unpleasant fact: most of us aren’t going to live more than 80 years or so. We don’t have time to waste. For some folks, knowing how to use and apply the functionality that surrounds the Lambert function to give it power is enough to make life worth living. Count me in.
No one needs to wade through the jungles of series expansions and transcendental integrals. Let math apps do the tedious work, knowing full well that any interested person can master whatever they choose if necessary, but someone already did the work. Why duplicate the effort?
I want to solve novel functions — complicated formulas that transcend algebra. Understanding the process that solves these equations is fascinating. It’s not as rewarding to tread over mathematically esoteric ground already mapped by experts who are far more able than people who spend most of their time working in other fields.
Here is the solution process:
What we know:
IF y = f(x) = xex
THEN x = ω(y) [where “ω” is the Lambert W function]
Solve:
![]()
![]()
![]()
![]()
LET x = et
(1) THEN ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2) ![]()
![]()
Referring to “what we know“, the equation is now in the desired form
y = xex
where “y” is equal to ![]()
![]()
![]()
We are now free to use the omega operator to “invert” the equation into the following form: x = ω(y)
(3) (-3t) = ω ![]()
![]()
![]()
(4) ∴ t = ![]()
![]()
Notice that we have worked through step (4) of the strategy. I don’t like the way the formula generator writes the Greek letter omega (ω), because it’s hard to read. From here on, I will sometimes use “W” instead of “ω” for readability. It shouldn’t confuse anyone. In this essay, consider W and ω the same symbol, please.
On to step (5).
SINCE x = et
(5) THEN ![]()
![]()
I need to know what -ω0(-1/8) equals so that I can use it to compute one of the values of “x”. As mentioned above, three more omegas with three other subscripts (-1, -2, and 1) are needed to compute all four of the solutions to this equation.
How does anyone know how many solutions the original function has? How does anyone know what subscripts are required?
This is where someone who doesn’t have a masters degree in mathematics needs a math app like Wolfram Alpha or its cousin, Mathematica. Otherwise, they have to work series expansions or difficult integrals to derive the omega values associated with (-1/8). Who wants that? Not me.


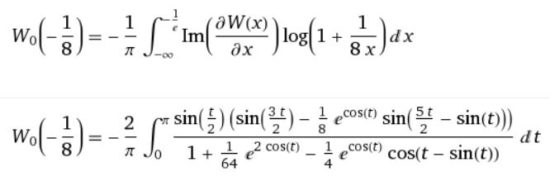
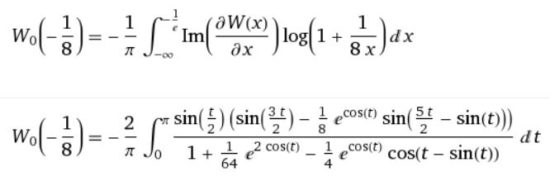
OK. In WolframAlpha, you get the omega value ω0 for (-1/8) by writing the expression -W[0,-1/8] in the input line at the top of the page. It shoots out the answer and links to its derivation.
It’s so simple. Other math apps might use different notation. I don’t know, because I don’t use other apps.
Inside the brackets, the “0” is the subscript on ω, and the “-1/8” is the “y” value, right? So, in addition to -W[0,-1/8] it is necessary to input:
-W[-1,-1/8]
-W[-2,-1/8]
-W[1,-1/8]
to obtain the three other omega values, right?
The omega values returned are the following:
1.4442135…
3.2616856…
4.21446… + 7.33231…i
4.21446… – 7.33231…i
The ω function values for -1/8 are two real numbers and two complex numbers. I am going to solve the original equation for only the first real number omega value to demonstrate the method.
Here it is:
INPUT -W(-1/8) or -W[0,-1/8], both work for ω0
(6) OUTPUT +0.14442135…
COMPUTE ![]()
![]()
t = ![]()
![]()
SINCE x = et
THEN x = e.04814…
(7) SOLUTION x = 1.04931755…
CHECKING ![]()
![]()
![]()
![]()
BY SUBSTITUTION ![]()
![]()
VERIFICATION .04814… – .04814… = 0
CONCLUSION: The transcendental equation which is the focus of this essay can easily be solved and verified by simply punching the equation into the input field of a math app like Wolfram Alpha or Mathematica and reading off the answers.
We didn’t perform the simple procedure, because I wanted to share how the Lambert W function fits into the solution process for solving equations.
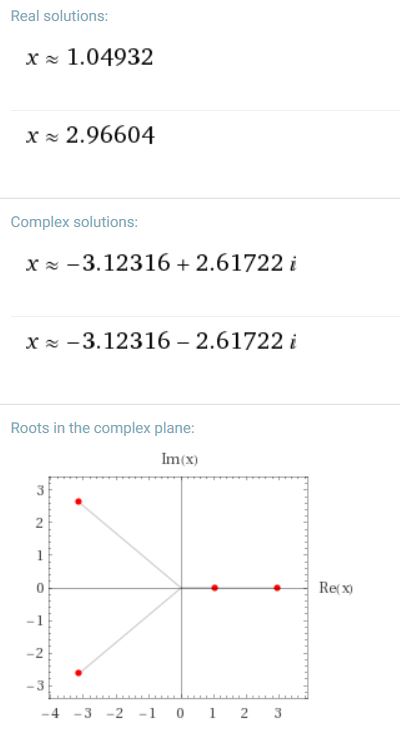
In truth, all four ω values must be gathered so that the three other “x” values of the original equation can be derived.
In this example, one of the other solutions will be real; the other two, complex. The screenshot below from Wolfram Alpha demonstrates how these four values are displayed. Of course, by clicking links the app will reveal much more.

I would be remiss to not mention a famous formula for calculating to what number a fraction raised to successive powers of the same fraction converges.
(The range of numbers where this formula actually works is between e−e and e1/e, that is, between .065988… and 1.444667861… .)
Take a number like ½ (0.5). Raise it to the 0.5 power; raise it again and again to the same power over and over an infinite number of times; the number will converge to a specific value.
What number? How in the world could anyone figure it out without repeating the power-raising process an annoying number of times?
It turns out that a formula involving the Lambert W Function yields up the answer easily.
The formula is:
# = ![]()
![]()
Put the following expression into the INPUT line of WolframAlpha:
-W[0,-ln(.5)] / [ln(.5)]
Click ” = ” — or hit “ENTER”.
The OUTPUT is: 0.6411857445049859844862…
Compare this result by taking the exponent (0.5) of 0.5 twenty times by hand (on a calculator). The answers will agree to 7 decimal places. Fifty “tetrations” will bring greater agreement if your calculator can parse the answer.
Who has the time?
Billy Lee
NOTE from the EDITORIAL BOARD: Billy Lee was unable to find an appropriate video about the Lambert function on YouTube, or we would have posted it. Most folks capitalize the Greek letter omega (Ω), but in this essay, Billy Lee didn’t, preferring instead to use little (ω), because it looks more like (W).
Who on the BOARD would dare argue?
Apparently, no one.
Another reason is that Ω is sometimes given the value 0.567143… , which is known as the omega constant. Why confuse things?
The video above starts a discussion of the Ω function at 16:30. The Lambert W function is derived for ΩeΩ = 1 at 18:00. The first sixteen minutes and thirty seconds show how to use Newton’s Method to solve the equation. Some readers might want to skip the first 16 minutes; others will enjoy them.
Who knows?

